Dhrubajyoti Ghosh

Snapshots of shared memory

We have an \( n \)-length array \( \texttt{A} \) where each \( \texttt{A[i]} \) is updated by a different writer \( \texttt{W[i]} \). There is also a reader \( \texttt{R} \) who reads \( \texttt{A} \) from left to right and whose task is to return a snapshot reflecting the contents of \( \texttt{A} \) at some time.

The task is not straightforward. Due to the ever-changing nature of \( \texttt{A} \), simply reading it sequentially might return a snapshot that \( \texttt{A} \) was never equal to!

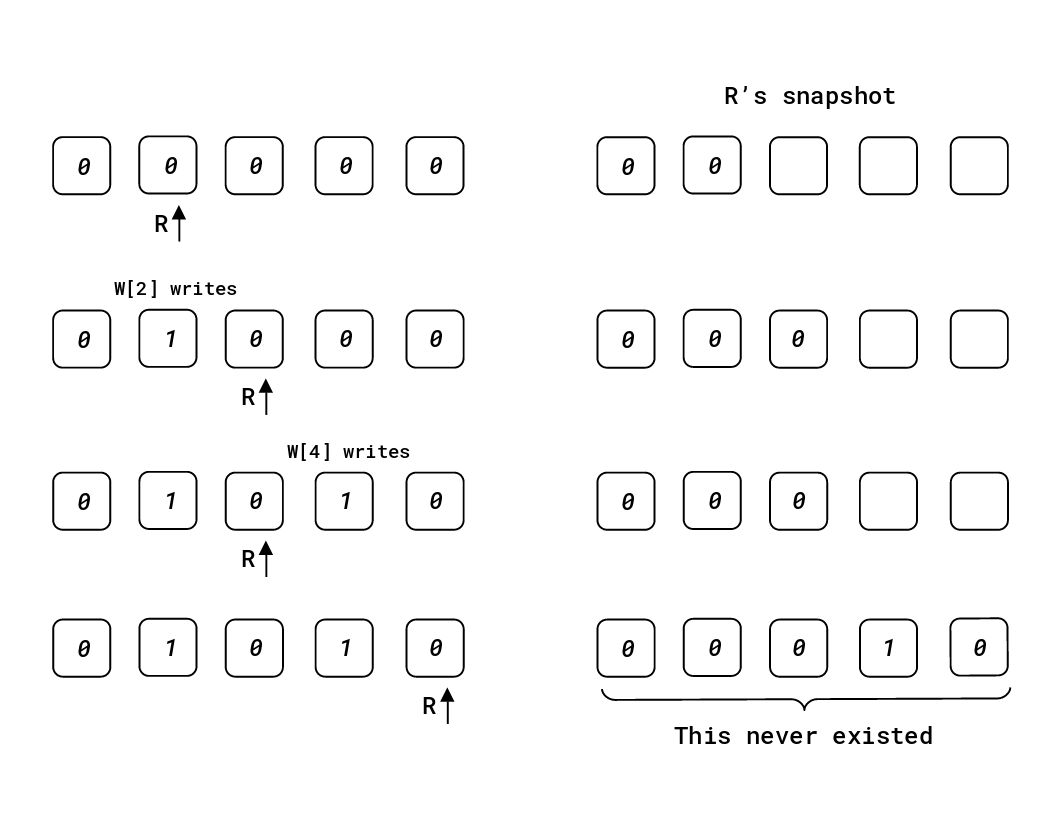
The reader and writers need to work together to avoid this issue. It will be assumed that

1. the read of a single cell and a write to that cell do not overlap (think of them as atomic operations),
2. \( \texttt{R} \) should not return an 'old' valid snapshot, i.e. in the order \( \texttt{A=V1} \rightarrow \texttt{A=V2} \rightarrow \texttt{R's read} \) (with none of the events overlapping), \( \texttt{R} \) should not return \( \texttt{V1} \) as its snapshot.

Solution #1

In addition to writing a value to its cell, the writer also includes the timestamp.

The reader keeps reading the array in an indefinite loop (call each iteration a \( \texttt{collect} \) ), until two consecutive \( \texttt{collects} \) return the same snapshot. This snapshot is valid since it must have existed at any point in the time gap between the two \( \texttt{collect} \)s (timestamping the values is crucial in ensuring this).

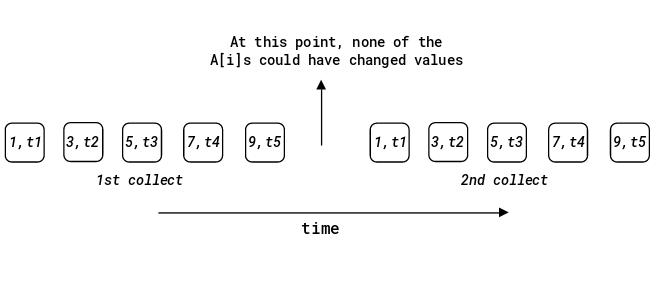
The issue here is that \( \texttt{R} \) might keep on iterating this loop forever because the \( \texttt{collect} \)s could always keep changing.

Solution #2

In #1, the writers were causing the trouble and did not bother to do anything about it. They will have to 'help' \( \texttt{R} \) by taking a valid snapshot of \( \texttt{A} \) before writing (so a write is now a read followed by the update), and if \( \texttt{R} \) is stuck on the loop for too long, it uses those snapshots. At this point some things are not clear:

1. how the writers manage to always take a valid snapshot, and
2. how and when \( \texttt{R} \) chooses among these snapshots so as to not violate B.

The solution is a recursive one. A read \( \texttt{r} \) operates as follows (note that writers and \( \texttt{R} \) both implement reads now):

• Keep repeating \( \texttt{collect} \) as before. If two consecutive \( \texttt{collect} \)s are the same, use that \( \texttt{collect} \) as it is a valid snapshot. If this does not happen, eventually there must be some writer \( \texttt{W} \) who has changed(/updated) the array twice (PHP).
• This means \( \texttt{W} \) must have executed an entire write (starting after its first update) within the interval in which read \( \texttt{r} \) was executed.
• This is the cue for recursion, since \( \texttt{W} \)'s write has a read embedded in it. End the definition of \( \texttt{r} \) by requiring that IF \( \texttt{W} \)'s (embedded) read had returned a snapshot to \( \texttt{W} \), then \( \texttt{r} \) should use that snapshot, otherwise it returns nothing.

In fact, \( \texttt{W} \)'s embedded read SHOULD have returned a snapshot and moreover the snapshot is valid (meaning \( \texttt{r} \) always returns a valid snapshot). To see this, look at \( \texttt{W} \)'s embedded read - either it must have had two consecutive \( \texttt{collect} \)s in which case we do have a valid snapshot, or there must be a writer \( \texttt{W'} \) whose write interval falls within \( \texttt{W} \)'s embedded read interval. Clearly \( \texttt{W'} \neq \texttt{W} \). Apply the same reasoning to \( \texttt{W'} \). How long can this go on recursively? There are at most \( n \) writers. Down the line, we will run out of writers and there will be some super-embedded read which finds two consecutive equal \( \texttt{collect} \)s and thus has a valid snapshot. This snapshot gets carried up the recursion chain and is returned by \( \texttt{r} \).

Illustrations for #2 coming up.

References

• Atomic Snapshots of Shared Memory, Yehuda Afek, Hagit Attiya, Danny Dolev, Eli Gafni, Michael Merritt, Nir Shavit
• The Art of Multiprocessor Programming, by Maurice Herlihy and Nir Shavit.